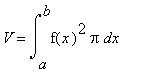Man beschreibt die Mantellinie des Fasses durch eine geeignete ganzrationale ( meistens durch eine quadratische) Funktion. Nun wählt man ein bestimmtes Intervall [a;b] auf der Kurve, durch welches sich die Mantellinie des Fasses besonders gut darstellen läßt. Beim Rotieren der Fläche unter dieser Kurve ( Fläche zwischen der Kurve und der x -Achse) in dem gewählten Intervall ensteht ein Körper, nämlich ein Faß.
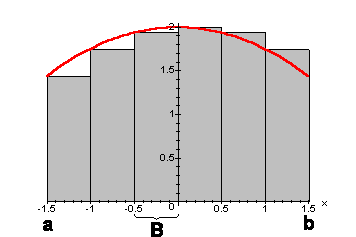Um dessen Volumen zu bestimmen, benutzt man die oben genannte Fläche. Dabei liegt der Trick der ganzen Idee im Unterteilen der Fläche in Rechtecke mit gleicher Breite (Es ginge auch mit unterschiedlich breiten Rechtecken, aber für die Rechnung später sind gleich breite Rechtecke einfach praktischer); um gleich breite Rechtecke zu erhalten, teilt man einfach das Intervall durch eine (natürliche) Zahl n, dann ist die Breite 
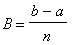und die Höhe der Rechtecke ist der Funktionswert an der Anfangsstelle jedes Rechtecks - das erste Rechteck hätte also die Höhe f(a).Läßt man diese Rechtecke rotieren, erhält man Zylinder, die den Faß nährungsweise beschreiben. Das Volumen eines solchen Zylinders berechnet man als das Produkt aus Pi, der Zylinderhöhe (in unserem Fall Breite B) und dem Quadrat des Zylinderradius, in unserem Fall f(a + k B):
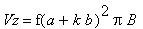
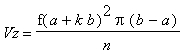
Die Summe der Zylindervolumina - daher der Begriff des "Untersummen", da ja die Rechtecke auch "unter" der Kurve sind - ergibt dann ungefähr den Faßvolumen:
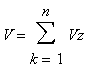
Wählt man n groß, so ist der Fehler sehr klein, da dann B klein ist und damit der Fehler zwischen einem Zylindervolumen und dem Volumen, das bei der Rotation der zu gehörigen tatsächlichen Fläche entsteht, klein ist.
Den exakten Rauminhalt des Fasses erhält, man wenn n unendlich groß ist; dann geht der Fehler gegen Null.
Wenn also B gegen Null geht, nennt man es Differential dx. Das Volumen läßt sich dann so berechnen:
