Lösung durch die Integralrechnung

Das Problem läßt sich heute mit Hilfe der Integralrechnung leicht lösen. Dabei stellt das Aufstellen einer geeigneten Funktion mit einer passenden Randkurve zum jeweiligen Faß das größte Hindernis dar. Man braucht also eine Funktion, deren Kurve die Mantellinie fast wahrheitsgetreu beschreibt.

Üblicherweise nimmt man zur Beschreibung solcher Mantellinien Abschnitte der Schaubilder quadratischer Funktionen. Eine geeignete Randkurve wäre z.B. die Kurve der Funktion 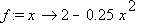im Intervall von -1 bis 1:
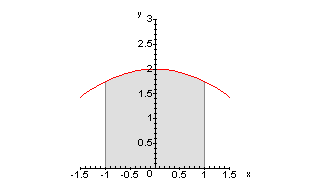Nimmt man nun die Fläche unter der Kurve im Abschnitt von -1 bis1 und läßt diese um die x-Achse rotieren, so erhält man einen Faß mit dem Bauchradius 2, der Weinlänge (Höhe) 2 und dem Kopfradius 1,75. (Die Begriffe sind der Fachsprache des Küferhandwerks entnommen).

Mit Hilfe der Integralrechnung kann man nun das Volumen eines Fasses vollkommen genau berechnen, im obigen Beispiel wären das 21.25811... Volumeneinheiten.

Herleitung | Mängel
Zurück zur Startseite