Herleitung der Keplerschen Faßregel
 Wie
kann man der Keplerschen Faßregel mathematischen Halt verleihen?
Wie
kann man der Keplerschen Faßregel mathematischen Halt verleihen?
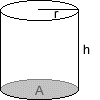
- Nun, stellen wir uns zunächst vor, das Faß wäre eine einfache
Tonne, hätte also einen geraden anstatt eines gewölbten seitlichen
Randes. Dann wäre das Volumen dieses Körpers einfacher zu berechnen,
nämlich als das Produkt aus der kreisförmigen Grundfläche
A und der Höhe h. Die Grundfläche wiederum ergibt sich aus dem
Produkt des Quadrats des Radius r mit der Kreiszahl Pi:
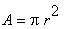 . Das Volumen
V wäre demnach
. Das Volumen
V wäre demnach
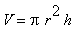 .
.
Wie aber berechnet sich das Volumen eines Fasses, das ja einen Bauch und
keinen geraden Rand hat?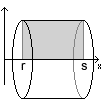
- Wir bedienen uns eines einfachen, in der Mathematik oft angewandten Tricks:
Wir reduzieren das Problem zunächst auf ein einfacheres, eines welches
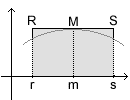
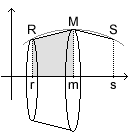
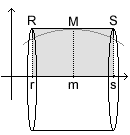
wir schon ohne große Mühe lösen können, nämlich auf die oben erwähnte Tonne; allerdings betrachten wir unsere Tonne nun auf eine andere Weise: wir stellen sie nicht mehr auf, sondern wir legen sie auf die Seite, oder noch besser: wir hängen sie entlang ihrer Mitte auf, so daß die Seiten nun parallel zum Boden liegen. Zum Aufhängen benutzen wir keine Schnur, sondern die x-Achse eines Koordinatensystems zwischen den Stellen r (Mitte des Faßdeckels) und s (Mitte des Faßbodens).
Den Anfangs- und den Endpunkt des Bogens nennen wir entsprechend R bzw. S.
Den Radius r der Tonne drücken wir über eine Funktion f aus, dann errechnet sich das Volumen nun als 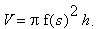
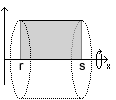 Stellen wir uns die Tonne aber einmal nicht als aufgehängten Körper vor,
sondern als den Raum, den ein um die x-Achse rotierendes Rechteck, dessen
unterer Rand die x-Achse und dessen oberer Rand die Strecke RS bildet, einnimmt.
So merken wir schnell, daß es die Fläche des Rechteckes ist, die
das Volumen des "Rotationskörpers", also in unserem Falle des Fasses,
bestimmt. Die sogennante "Kepplersche Faßregel" gibt uns den Inhalt
solcher Flächen an.
Stellen wir uns die Tonne aber einmal nicht als aufgehängten Körper vor,
sondern als den Raum, den ein um die x-Achse rotierendes Rechteck, dessen
unterer Rand die x-Achse und dessen oberer Rand die Strecke RS bildet, einnimmt.
So merken wir schnell, daß es die Fläche des Rechteckes ist, die
das Volumen des "Rotationskörpers", also in unserem Falle des Fasses,
bestimmt. Die sogennante "Kepplersche Faßregel" gibt uns den Inhalt
solcher Flächen an.
 Wie
ersetzen wir unsere Tonne nun wieder durch das Faß?
Wie
ersetzen wir unsere Tonne nun wieder durch das Faß?
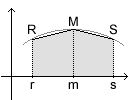
- Gerade dabei ergibt sich allerdings ein Problem: Mit einer geeigneten Funktion
f können wir zwar leicht den gewölbten Rand des Fasses nachzeichnen,
um so zu einer geeigneten Rotationsfläche zu gelangen. f(x) gibt uns
den Radius des Fasses aber nur an einer einzigen Stelle (nämlich an
der Stelle x) an. Daher unterteilen wir den Bogen, den die Funktion f
nachzeichnet, in zwei Abschnitte. Idealerweise wählen wir die halbe
Höhe des Fasses als Trennstelle, die Stelle nennen wir m, den entsprechenden
Punkt auf dem Bogen (bzw. dem Faßrand) nennen wir M. Dann verbinden
wir die Punkte R und M sowie M und S jeweils durch Strecken, um den Bogen
grob schematisiert nachzeichnen zu können.
Zwar verlieren wir durch die "Schematisierung" (man sagt in der Mathematik:
"Approximation" oder "Annäherung an die Kurve") an Genauigkeit, dafür
können wir die erhaltene Rotationsfläche des manipulierten Fasses
leicht errechnen: Beide Abschnitte stellen je ein Trapez dar, dessen
Flächeninhalt A gleich dem Produkt aus der Länge der Grundseite,
also in unserem Fall der halben Höhe h des (stehenden) Fasses, und der
mittleren Höhe des Trapezes, also aus dem arithmetischen Mittel von
f(r) und f(s): 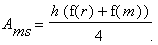
Analog erhalten wir für den zweiten Abschnitt den Flächeninhalt
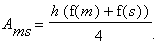
Beide zusammen ergeben die Rotationsfläche der gesamten Figur:
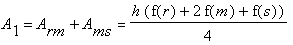
Bei der Schematisierung ist die Rotationsfläche und damit auch unser
Faß etwas zu klein geraten, da die Strecken RM und MS unterhalb des
Bogens verlaufen. Können wir diesen Fehler wieder etwas ausgleichen?
- Als Ausgleich zu dem Verlust an Rotationsfläche, der bei der
Schematisierung entstanden ist, gibt es ein weiteres Verfahren, mit dem man
die Fläche unterhalb des Bogens ebenfalls schematisiert darstellt; hierbei
wird die Fläche aber vergrößert, was als Ausgleich zum Verlust
beim ersten Verfahren dienen soll:
 Es ist einfacher, aber auch ungenauer als das erste Verfahren, denn wir wählen
diesmal als Rotationsfläche einfach das Rechteck der Höhe f(m)
zwischen den Stellen a und b, das also genau so lang ist wie das (stehende)
Faß hoch; der Flächeninhalt dieses Rechtecks ist demnach
Es ist einfacher, aber auch ungenauer als das erste Verfahren, denn wir wählen
diesmal als Rotationsfläche einfach das Rechteck der Höhe f(m)
zwischen den Stellen a und b, das also genau so lang ist wie das (stehende)
Faß hoch; der Flächeninhalt dieses Rechtecks ist demnach 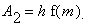
Es bleibt die Frage, wie wir beide Verfahren miteinander kombinieren
sollen.
- Nun, da das erste Verfahren um den Faktor 2 genauer ist, denn hier haben
wir das Faß zur Schematisierung in zwei Abschnitte unterteilt, verrechnen
wir es einfach mit dem zweiten, bei dem wir das gesamte Faß sozusagen
in einem Abschnitt schematisiert haben, in der Wertigkeit 2 zu 1:
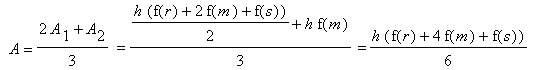
Bei der erhaltenen Näherungsformel handelt es sich um die "Keplersche
Faßregel".
Um aber das Volumen eines Fasses zu berechnen, müssen wir noch weiter
überlegen, denn diese Keplersche Faßregel gibt uns ja offensichtlich
nur die halbe Querschnittsfläche eines Fasses an, nicht aber dessen
Volumen.
Wie berechnet man aber das Volumen nach Kepler?
Nun, wir vollziehen wieder jeden Schritt beider Näherungen nach:
 Bei der ersten Näherung erhalten wir zwei Trapeze. Lassen wir diese um die
x-Achse rotieren, so erhalten wir je einen Kegelstumpf. Das Volumen eines
Kegelstumpfes erhält man aus
Bei der ersten Näherung erhalten wir zwei Trapeze. Lassen wir diese um die
x-Achse rotieren, so erhalten wir je einen Kegelstumpf. Das Volumen eines
Kegelstumpfes erhält man aus 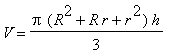 , wobei R und r die Radien, h die Höhe des Kegelstumpfes sind. Bei unseren beiden Trapezen wären das also
, wobei R und r die Radien, h die Höhe des Kegelstumpfes sind. Bei unseren beiden Trapezen wären das also 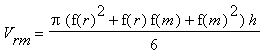 und
und 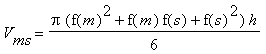 .
.
Beide zusammen ergeben wieder unsere erste Näherung:
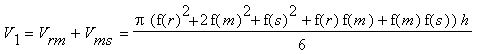
 Um die zweite Näherung zu erhalten, lassen wir das umschriebene Rechteck
rotieren und bekommen so einen Zylinder bzw. eine Tonne. Deren Flächeninhalt errechnet sich als
Um die zweite Näherung zu erhalten, lassen wir das umschriebene Rechteck
rotieren und bekommen so einen Zylinder bzw. eine Tonne. Deren Flächeninhalt errechnet sich als 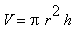 , wobei r der Radius und h die Höhe ist. In unserem Beispiel wäre
f(m) der Radius, das Volumen der zweiten Näherung folglich
, wobei r der Radius und h die Höhe ist. In unserem Beispiel wäre
f(m) der Radius, das Volumen der zweiten Näherung folglich 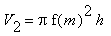 .
.
Verrechnen wir wieder beide Näherungen in der Wertung 2:1 meiteinander,
so erhalten wir als endgültige Näherung für das Volumen 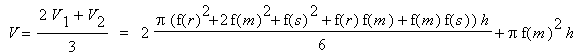
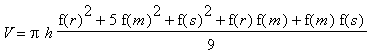 .
.
Für den Spezialfall f(r) = f(s) ergibt sich dann
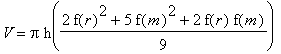 .
.
Zurück zur Keplerschen Faßregel
Zurück zur Startseite
 Wie
kann man der Keplerschen Faßregel mathematischen Halt verleihen?
Wie
kann man der Keplerschen Faßregel mathematischen Halt verleihen?
 Stellen wir uns die Tonne aber einmal nicht als aufgehängten Körper vor,
sondern als den Raum, den ein um die x-Achse rotierendes Rechteck, dessen
unterer Rand die x-Achse und dessen oberer Rand die Strecke RS bildet, einnimmt.
So merken wir schnell, daß es die Fläche des Rechteckes ist, die
das Volumen des "Rotationskörpers", also in unserem Falle des Fasses,
bestimmt. Die sogennante "Kepplersche Faßregel" gibt uns den Inhalt
solcher Flächen an.
Stellen wir uns die Tonne aber einmal nicht als aufgehängten Körper vor,
sondern als den Raum, den ein um die x-Achse rotierendes Rechteck, dessen
unterer Rand die x-Achse und dessen oberer Rand die Strecke RS bildet, einnimmt.
So merken wir schnell, daß es die Fläche des Rechteckes ist, die
das Volumen des "Rotationskörpers", also in unserem Falle des Fasses,
bestimmt. Die sogennante "Kepplersche Faßregel" gibt uns den Inhalt
solcher Flächen an.
 Wie
ersetzen wir unsere Tonne nun wieder durch das Faß?
Wie
ersetzen wir unsere Tonne nun wieder durch das Faß? Es ist einfacher, aber auch ungenauer als das erste Verfahren, denn wir wählen
diesmal als Rotationsfläche einfach das Rechteck der Höhe f(m)
zwischen den Stellen a und b, das also genau so lang ist wie das (stehende)
Faß hoch; der Flächeninhalt dieses Rechtecks ist demnach
Es ist einfacher, aber auch ungenauer als das erste Verfahren, denn wir wählen
diesmal als Rotationsfläche einfach das Rechteck der Höhe f(m)
zwischen den Stellen a und b, das also genau so lang ist wie das (stehende)
Faß hoch; der Flächeninhalt dieses Rechtecks ist demnach 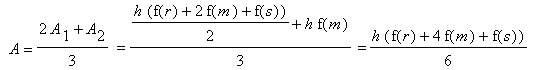
 Bei der ersten Näherung erhalten wir zwei Trapeze. Lassen wir diese um die
x-Achse rotieren, so erhalten wir je einen Kegelstumpf. Das Volumen eines
Kegelstumpfes erhält man aus
Bei der ersten Näherung erhalten wir zwei Trapeze. Lassen wir diese um die
x-Achse rotieren, so erhalten wir je einen Kegelstumpf. Das Volumen eines
Kegelstumpfes erhält man aus 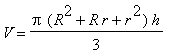 , wobei R und r die Radien, h die Höhe des Kegelstumpfes sind. Bei unseren beiden Trapezen wären das also
, wobei R und r die Radien, h die Höhe des Kegelstumpfes sind. Bei unseren beiden Trapezen wären das also 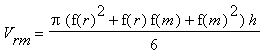 und
und 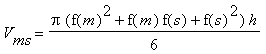 .
.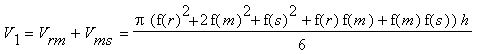
 Um die zweite Näherung zu erhalten, lassen wir das umschriebene Rechteck
rotieren und bekommen so einen Zylinder bzw. eine Tonne. Deren Flächeninhalt errechnet sich als
Um die zweite Näherung zu erhalten, lassen wir das umschriebene Rechteck
rotieren und bekommen so einen Zylinder bzw. eine Tonne. Deren Flächeninhalt errechnet sich als 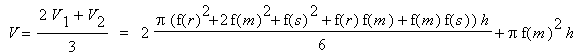
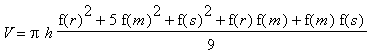 .
.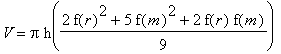 .
.