Vergleich der Genauigkeit anhand einiger Beispiele
|
|
Die einzelnen Methoden: Zur Visiermethode Zur Keplerschen Faßregel Zur Integralrechnung Zurück zur Startseite |
Genauigkeitsvergleich der verschiedenen Methoden
Im folgenden wollen wir die Genauigkeit der verschiedenen Methoden an mehreren
Beispielen testen. Zum Vergleich ziehen wir aber nur die Visiermethode, die
Keplersche Lösung und die der Integralrechnung als Kontrollinstrument
heran, da sich erwiesen hat, daß keine der praktischen Lösungen
die Aufgabenstellung erfüllt.
Vergleich der Genauigkeit anhand einiger Beispiele
|
|
Die einzelnen Methoden: Zur Visiermethode Zur Keplerschen Faßregel Zur Integralrechnung Zurück zur Startseite |
im Intervall von -1,5 bis 1,5:
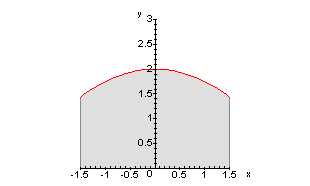Diese
Kurve dürfte Ihnen schon bekannt vorkommen, wir haben sie schon bei der Vorstellung der Integralrechnung verwendet, nur hatten wir da einen kleineren
Bereich, nämlich im Intervall von -1 bis 1 gewählt. Nun wollen wir Genauigkeit der einzelnen Methoden exemplarisch an dieser Kurve überprüfen.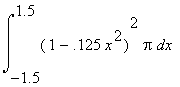
= 31.22694010 RE (=Raumeinheiten).
Beispiel 2
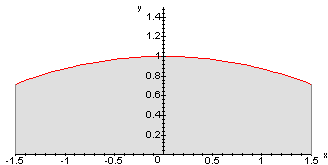
Unser nächstes Faß hat die Kurve der Funktion
im Intervall
von -1,5 bis 1,5 als Mantelinie.
1) Integralrechnung
Der genaue Rauminhalt des Fasses lautet nach der Berechnung mit Hilfe der
Integralrechnung
V =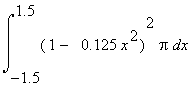 
=
7.806735026 RE.
2) Visiermethode
Nach dieser Methode bekommen wir folgendes Ergebnis:
V = 7.123114014 RE.
Hier müssen wir eine Abweichung von 0,683621012 RE bzw. 8,86 % hinnehmen.
3) Keplersche Lösung
Die Keplersche Formel gibt uns dieses Volumen an:
V = 7.823302019 RE.
Man errechnet dann ein Unterschied von 0,0165666993 RE bzw. von 2,1 %.
Beispiel 3
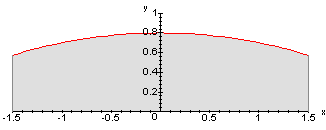
In diesem Beipiel benutzen wir die Kurve der Funktion
als Randkurve,
wobei wir sie auch im Intervall von -1,5 bis 1,5 betrachten.
1) Integralrechnung
Mit diesem Lösungsweg berechnen wir für das exakte Volumen
V =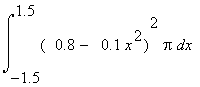 
= 4.996310416 RE.
2) Visiermethode
Wir messen einen Abstand vom Spundloch zur untersten Bodenencke von s
= 2.034852575 LE. Daraus errechnet sich ein Volumen von V = 5.055336868 RE.
Das ist eine Abweichung von 0.059026452 RE bzw.1,18%.
3) Die Keplersche Lösung
ist wieder einmal genauer als die Visiermethode: Mit einem Volumen
von V = 5.006913292 RE beträgt die Abweichung nur 0,010602876 RE oder
0,21%.
Beispiel 4
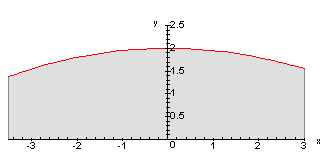Nun
beschreiben wir die Mantellinie eines Fasses durch das Schaubild der Funktion
im Bereich
von -3,5 bis 3. Dies stellt nun ein Faß dar, dessen Deckel und Boden
verschieden groß sind.
1) Integralrechnung
Wir beginnen wieder mit der Integralrechnung, um die exakte Lösung an
den Anfang stellen zu können, denn das eröffnet uns die
Möglichkeit, diese als Vergleichsmaßstab anzusetzen. Diese exakte
Lösung ist
V =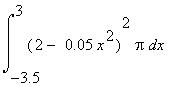 
=
68.25353841 RE.
2) Visiermethode
Hier wird das Ergebnis wieder ungenau: Für den Abstand messen wir s
= 4.870847591, daraus errechnet sich ein Volumen von V = 69.33697212 RE.
Dies entspricht einer Abweichung von 1,08343371 RE oder 1,59 %.
3) Keplersche Lösung
Wieder einmal ist dies die bessere Näherung: 68.38761788 RE sind ein
respektables Ergebnis. Denn das stellt eine Abweichung von nur 0,13407947
RE oder weniger als 0,20 % dar.
